Критерии оптимального обнаружения

Перед тем, как находить оптимальное решение, необходимо определить критерий, согласно которому оно должно быть оптимизировано. Ввиду случайного характера анализируемых процессов, оптимум определяется не по отдельным их реализациям, а в среднем, по многим реализациям.

Рассмотрим наиболее распространенные критерии оптимальности обнаружения:

. Критерий минимума среднего риска (критерий Байеса). Выявляется полная группа всех возможных сочетаний событий и решений, т.е. в данном случае: - безусловные совместные вероятности.

Сумма их безусловных вероятностей:

.

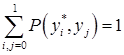Далее назначается плата (риск) для ошибок каждого вида (для безошибочных решений плата равна 0):

Определяется средний риск:

Безусловные вероятности ошибочных сочетаний могут быть выражены через их условные вероятности:

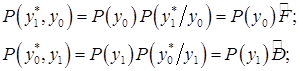
С учетом этого можно определить средний риск:

На основании этого соотношения определяется порог чувствительности приемного устройства, при котором минимален.

Характерным для этого и более частного критериев является этап назначения платы для каждого вида ошибок, который является результатом не строгого логического обоснования, а волевого эвристического определения коэффициента риска на основе предшествующего опыта и инженерной интуиции разработчика.

Все другие критерии оптимального обнаружения могут рассматриваться как частные случаи критерия минимального среднего риска.

. Критерий идеального наблюдателя (критерий Котельникова)

Предполагает равенство минимальных ошибок: . При этом: , и должны быть известны.

В частном случае равенства априорных вероятностей наличия и отсутствия сигнала , средний риск представляет собой среднеарифметическую ошибку: .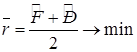

Этот критерий чаще применяется в системах передачи информации.

. Критерий Неймана-Пирсона

Задают предельно допустимое значение вероятности ложной тревоги и при условии определяют порог чувствительности приемного устройства, при котором обеспечивается максимальная вероятность правильного обнаружения .

Для иллюстраций сказанного рассмотрим рисунок 3. Приведены 4 реализации случайного колебания: первые две изображают шум на выходе согласованного фильтра, а две другие - сумму сигнала и шума. При этом установлен некоторый порог приемного устройства - . Шум в первой реализации не превышает порога. Во второй реализации, хотя сигнала и нет, однако выброс шума превышает порог. В третьей реализации сумма сигнала и шума превышает порог, в четвертой - не достигает порога.

Из рассмотренных случаев в первом и третьем случае будет принято правильное решение, а во втором и четвертом - нет. Если взять другой порог, то ситуация может измениться.

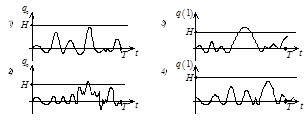
Рисунок 3

Кроме перечисленных, используются также критерии:

минимальной взвешенной вероятности ошибки;

Читайте также

Проектирование РЭА
При конструкторском проектировании РЭА (радиоэлектронной аппаратуры) решаются задачи, связанные с поиском наилучшего варианта конструкции, удовлетворяющего требованиям технического задан ...

Принцип работы оптоволоконных сканеров отпечатков пальцев
Идентификация по отпечаткам пальцев - на сегодня самая распространенная биометрическая технология. По данным International Biometric Group, доля систем распознавания по отпечаткам пальце ...

Проектирование спутниковой линии связи между городом Якутск и поселком Черский
Стремительное развитие космонавтики, успехи в изучении и исследовании околоземного и межпланетного космического пространства выявили весьма высокую эффективность использования околоз ...