Оценочные тесты

а) Критерий . Пусть результаты испытаний таковы, что их можно разделить на k категорий. Проводится п независимых испытаний. Обозначим вероятность того, что результат испытания попадет в s-ю категорию, как ps , а число испытаний, которые реально попали в s-ю категорию, как Ys . Сформируем статистику

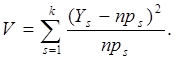(3.4)

Для оценки полученного результата используются таблицы распределения . В строках боковика (левого столбца) этих таблиц указано число степеней свободы, а в графах - вероятности, р. Смысл таблиц в следующем: если в некоторой строке таблицы в столбце находится число х, то это означает, что значение V, определяемое по вышеприведенной формуле при данном V, будет больше х с вероятностью p.

Например, для p= 5% и v = 10 таблица дает значение х = 18.31; это означает что V> 18.31 только в 5% всех случаев.

Для анализа полученного результата используются различные подходы. В [43] предлагается следующий. Если V меньше значения, соответствующего р = 99 %, или больше значения, соответствующего р = 1 %, то результаты бракуются, как недостаточно случайные. Если р лежит между 99 и 95% или между 5 и 1%, то результаты считаются "подозрительными", при значениях, заключенных между 95 и 90 % или 10 и 5 %, результаты "слегка подозрительны"; в остальных случаях результаты считаются случайными.

Однако при таком подходе будет забракована и по-настоящему случайная последовательность, для которой вероятность будет стремиться к 100%. Кроме того, нижняя граница прохождения тестов взята неоправданно малой. Поэтому логичнее оценивать результаты следующим образом. В зависимости от требования к генератору выбирается нижняя граница Рd. Результаты, для которых выполняется p<Pd , бракуются как неслучайные, в противном случае тест пройден.

б) Проверка частот. Тест проверяет равномерность появления символов в изучаемой последовательности. Подсчитывается, сколько раз встречается каждый символ - Ns (s=), после чего применяется критерий с числом категорий, равным 256, и вероятностями 1/256 в каждой категории

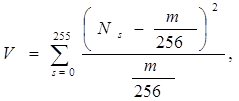(3.5)

где m - число анализируемых байтов. Полученные результаты анализируются при помощи таблицы распределения с числом степеней свободы, равным 255. Имеет смысл провести и проверку частот появления полубайтов. Для этого подсчитывается, сколько раз встречается каждый полубайт - Ns (s=), после чего применяется критерий с числом категорий, равным 16, и вероятностями 1/16 в каждой категории

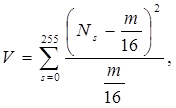(3.6)

где m - число анализируемых байтов. Полученные результаты анализируются при помощи таблицы, распределения с числом степеней свободы, равным 15.

в) Анализ перестановок. Тест проверяет равномерность распределения чисел в исходной последовательности. Разделим исходную последовательность на n групп по t элементов. В каждой группе возможно t! вариантов относительного расположения чисел. Подсчитывается, сколько раз встречается каждое конкретное относительное расположение - Ns , после чего применяется критерий с числом категорий, равным t!, и вероятностями 1/t! в каждой категории.

Читайте также

Проектирование двухвходовой КМОП-схемы дешифратора 2 в 4
КМОП (комплементарная логика на транзисторах металл-оксид-полупроводник; англ. CMOS, Complementary-symmetry/metal-oxide semiconductor) - технология построения электронных схем. В те ...

Моделирование мобильных систем связи
При организации сети сотовой связи для определения оптимального места установки и числа базовых станций, а также для решения других задач необходимо уметь рассчитывать характеристики сиг ...

Организация системы контроля доступа и видеонаблюдения в учреждении образования
Система контроля доступа - это совокупность программно-технических средств и чётко сформированной системы управления движением персонала и временем его нахождения на объекте. Основными ...