Линейные рекуррентные генераторы

Существует способ генерации последовательностей псевдослучайных чисел на основе линейных рекуррентных соотношений.

Рассмотрим рекуррентные соотношения через их разностные уравнения

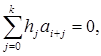(2.4)

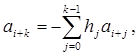(2.5)

где и каждое hi принадлежат полю GF(q).

Решением этих уравнений является последовательность элементов поля GF(q). Соотношение (2.5) определяет правило вычисления аk по известным значениям величин Затем по известным значениям находят ak+1 и т.д. В результате по начальным значениям можно построить бесконечную последовательность, причем каждый ее последующий член определяется из k предыдущих. Последовательности такого вида легко реализуются на компьютере, при этом реализация получается особенно простой, если все hi и ai значения 0 и 1 из поля GF(2).

На рис. 2.4 показана линейная последовательная переключательная схема, которая может быть использована для вычисления суммы и, следовательно, для вычисления значения аk по значениям k предыдущих членов последовательности.

Исходные величины помещаются в разряды сдвигового регистра, последовательные сдвиги содержимого которого соответствуют вычислению последовательных символов, при этом выход после i-го сдвига равен аi. Данное устройство называют генератором последовательности чисел, построенным на базе линейного сдвигового регистра с обратной связью (linear feedback shift register, LFSR).

Как правило, в реальных криптосхемах линейный регистр сдвига с обратной связью реализуется одной из двух различных конструкций, именуемых, соответственно, регистрами Фибоначчи и Галуа, но все наиболее важные теоретические результаты справедливы для обоих типов.

Рисунок 2.4 - Генератор с регистром сдвига

Регистры Фибоначчи

В литературе значительно чаще обращаются к регистрам Фибоначчи. Функция обратной связи здесь - простое сложение операцией XOR (исключающее или) определенных бит регистра. Перечень этих битов называется отводной последовательностью.

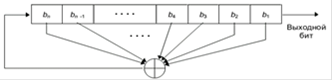
Рисунок 2.5 - Регистр Фибоначчи

битовый LFSR может находиться в одном из внутренних состояний. Это означает, что теоретически такой регистр может генерировать псевдослучайную последовательность с периодом битов. Только при определенных отводных последовательностях LFSR циклически пройдет через все внутренних состояний. Такие LFSR являются LFSR с максимальным периодом. Для того, чтобы LFSR имел максимальный период, многочлен, образованный от отводной последовательности и константы 1, должен быть примитивен по модулю 2. Степень многочлена является длиной сдвигового регистра. Примитивный многочлен степени - это неприводимый многочлен, который является делителем , но не является делителем для всех , являющихся делителями .

Читайте также

Организация системы контроля доступа и видеонаблюдения в учреждении образования
Система контроля доступа - это совокупность программно-технических средств и чётко сформированной системы управления движением персонала и временем его нахождения на объекте. Основными ...

Применение МПК в системах передачи информации
Каждое из трех предшествующих столетий ознаменовалось появлением какой-то технологии, развитие которой определяло прогресс в этом столетии. 18 век - механические системы, 19 - паровые ма ...

Модуль шестнадцатиразрядного двоичного реверсивного счетчика с параллельно-последовательным переносом, с предустановкой и выводом информации по два разряда, начиная с младшего
В настоящее время происходит компьютеризация практически во всех областях науки, техники, производства…Предпочтение отдается цифровым технологиям, которые считаются более продвинутыми и ...