Определение устойчивости нелинейной системы

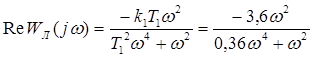
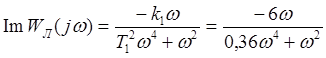
Гармонически линеаризованная передаточная функция нелинейного звена, согласно приложению, равна:

при a ≥ b2.

-Z(a) = 3.82()

Z(a) = - (a) =

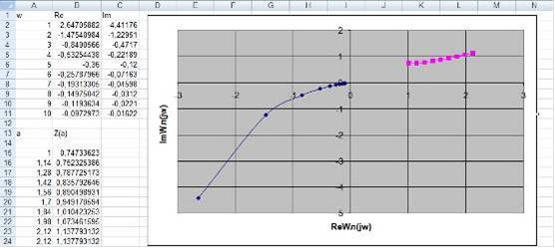
Рисунок 11.

Из рисунка 11 следует, что годографы не пересекаются в одной точке, что свидетельствует об отсутствии в системе автоколебаний и ее устойчивости.

Задача 9. Исследовать устойчивость состояния равновесия нелинейной системы (рис. 12). Параметры линейной части системы: Т1=NВ с, Т2=NВ-2,5 с, Т3=NВ·1,1 с, k1= NВ /10, k2=NВ·2. Для статической характеристики нелинейного звена: b=1, k3=NВ, где NВ - номер варианта.

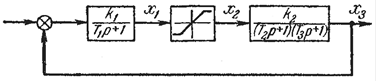
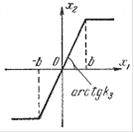
Рисунок 12.

Исходные данные:

Т1=Nв=26с;

Т2=Nв-2,5=6-2,5=3,5с;

Т3=Nв*1,1=6*1,1=6,6с;1= Nв/10=6/10=0,6;2= Nв*2=6*2=12;

b=1;3= NВ=6.

Решение

Амплитудно-фазовая характеристика линейной части:

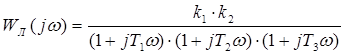
Умножаем на комплексно-сопряженные числа:

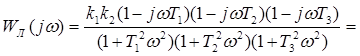
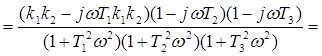
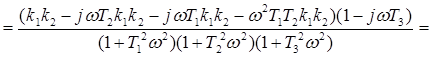
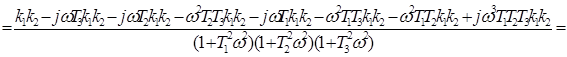
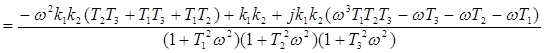
Разделяем вещественную и мнимую части:

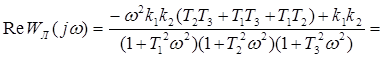
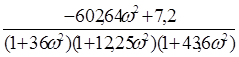
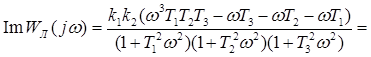
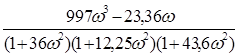
Гармонически линеаризованная передаточная функция нелинейного звена, согласно приложению, равна:

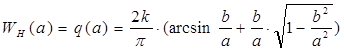при a>=b.

Z(a) =

Z(a) =

Получаем объединенный график годографов линейной и нелинейной частей:

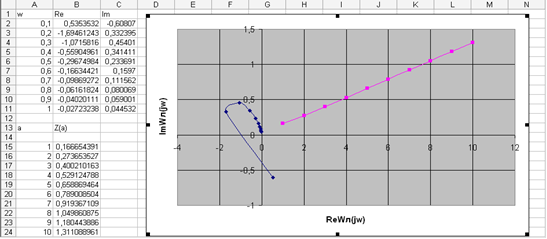
Рисунок 13.

Из рисунка 13 следует, что годографы не пересекаются в одной точке, что свидетельствует об отсутствии в системе автоколебаний и ее устойчивости.

дифференциальный уравнение устойчивость нелинейный

Читайте также

Моделирование радиомаячной системы посадки метрового диапазона с помощью программы Micro-Cap
Функциональные возможности использования авиации во многом определяются качеством решения задач навигации, в частности, уровнем развития устройств и систем радионавигации. Под термино ...

Проектирование устройства для измерения статических характеристик электромагнитного двигателя
Ветер - это горизонтальное перемещение, поток воздуха параллельно земной поверхности, возникающее в результате неравномерного распределения тепла и атмосферного давления и направленное и ...

Разработка конструкции линейного коммутатора
Радиоэлектронная аппаратура (РЭА), в основу функционирования которой положены принципы электроники, строится на базе электронных компонентов различного назначения (микросхем, резисторов, ...