Определение устойчивости нелинейной системы

Задача 1. Составить нелинейные дифференциальные уравнения следящей системы (рисунок 1)

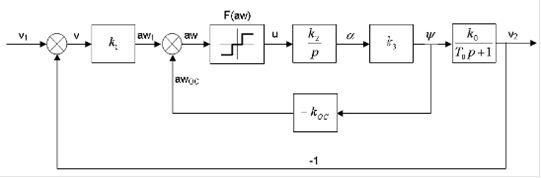
Рис. 1. Структурная схема следящей системы.

Исходные данные:

Т0=Nв/10=6/10=0,6;

k1=Nв=6;

k2=Nв*2=6*2=12;

k3=Nв/2=6/2=3

k0=Nв*1,5=6*1,5=9;

koc=Nв*2,5=6*2,5=15.

Решение

Уравнение чувствительного элемента:

aw1=k1*v;

v=v1-v2;

aw1=k1*(v1-v2)

Уравнение релейного усилителя:

u=F(aw); при koc = 0=aw1-awoc

Уравнение линейного усилителя:

αp=k2u;

Уравнение исполнительного механизма:

φ=k3*α

Уравнение редуктора:

(T0p+1)*v2=k0*φ

Уравнение обратной связи (тахогенератор):

awoc=koc*φ

Выражаем относительно выходной переменной aw:

=

Задача 2. Построить фазовый портрет системы

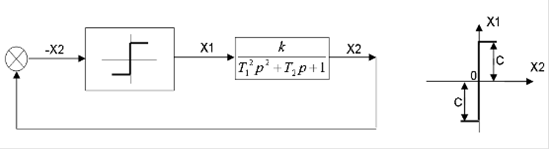
Рисунок 2.

Данные:

Т12=Nвар/10=6/10=0,6с;

Т2= Nвар/2=6/2=3с;

k= Nвар=6;

с=2.

Уравнения замкнутой нелинейной системы:

при х2>0 (1)

при х2<0 (2)

Заменяем: x2 = x

(0,62p2 + 3p +1) * x = -6 * 2

(0,36р2 + 3р + 1) * x = -12

Заменяем:

p =

( +1) x = -12

Заменяем:

; .

ydy + 3y + x = -12 => 0,36 + 3y + x = -12

Переносим x на правую сторону:

+ 3y = -12 - x

Переносим dy на правую сторону:

dx =

Интегрируем:

x = ln (- 3 - 12 - x) + C1

x = ln (- 3 + 12 - x) + C2

Упрощаем:

Читайте также

Разработка конструкции линейного коммутатора
Радиоэлектронная аппаратура (РЭА), в основу функционирования которой положены принципы электроники, строится на базе электронных компонентов различного назначения (микросхем, резисторов, ...

Разработка микропроцессорного контроллера для контроля ритма дыхания больного
В последнее время микропроцессорные средства вычислительной технике стало широко применяться в приборах бытовой техники, различных контрольно-измерительных устройствах, системах управлен ...

Организация системы контроля доступа и видеонаблюдения в учреждении образования
Система контроля доступа - это совокупность программно-технических средств и чётко сформированной системы управления движением персонала и временем его нахождения на объекте. Основными ...