Графические тесты

а) Гистограмма. Гистограмма позволяет определить равномерность распределения символов в тестируемой последовательности, а также оценить частоту появления конкретного символа. Данный тест незаменим при проверке последовательности на "случайность", а также при исследовании генераторов с произвольным законом распределения символов. Для того чтобы последовательность удовлетворяла свойствам случайности, необходимо, чтобы в ней присутствовали все символы, при этом разброс частот появления символов стремился к нулю. Рассматриваемый тест может принести пользу также в тех случаях, когда оценивается качество последовательности с законом распределения, отличным от равномерного, либо последовательности, в которой некоторые символы вообще отсутствуют, и т. д.

б) Распределение на плоскости. Тест позволяет оценивать равномерность и независимость распределения символов в исследуемой последовательности. Для построения графической зависимости на поле размером 256х256 наносятся точки с координатами

(Qi; Qi+1)

где Qi, - i-й элемент последовательности, , т - длина последовательности. Далее анализируется полученная картина. В случае некачественной последовательности точки распределены неравномерно, либо наблюдается некий узор.

Для последовательностей большой длины (порядка 700 Кб и выше) положительным результатом считается график, представляющий собой абсолютно черный квадрат.

в) Байтовая АКФ. Тест проверяет взаимонезависимость элементов изучаемой последовательности на основе анализа всплесков корреляции. Для расчета автокорреляционной функции последовательность нормируется. Пусть [q7…q1q0] -двоичная запись элемента последовательности длиной m, qj {0, 1}, . Тогда нормированное значение этого элемента вычисляется как

(3.1)

После этого вычисляются всплески корреляции

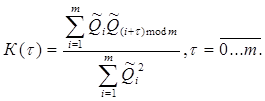(3.2)

Нетрудно заметить, что при = 0 и = m значение К ()= 1. Во всех остальных случаях для качественной ПСП значения К() должны стремиться к нулю.

г) Битовая АКФ. Тест проверяет взаимонезависимость битов последовательности. Сначала двоичное представление последовательности нормируется: 1 1, 0 -1. Затем вычисляются всплески корреляции по формуле

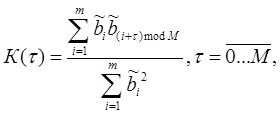(3.3)

где М - размер последовательности в битах, а - i-й бит нормированной последовательности. При =0 и = М значение К ()= 1. Во всех остальных случаях для качественной ПСП значения К () должны стремиться к нулю.

д) Проверка на монотонность. Тест проверяет равномерность распределения символов в изучаемой последовательности на основе анализа длин участков возрастания и убывания. В качественной ПСП разброс длин этих участков должен стремиться к нулю.

Читайте также

Проектирование релейной защиты и автоматики
В электрической системе имеются следующие источники: ТЭЦ-1, ТЭЦ-2, ТЭЦ-3, ТЭЦ-4, ТЭЦ-5, ГРЭС, СарГЭС и БАЭС. ТЭЦ-1, ГРЭС допускается отдельно не учитывать, так как их мощность по сравнению с ...

Разработка компьютерной сети по технологии ArcNet с подключением к Internet
Организация компьютерных сетей. Назначение: Создание компьютерных сетей вызвано практической потребностью пользователей удаленных друг от друга компьютеров в одной и той же информ ...

Назначение и виды ударно-контактных извещателей
Извещатели ударно-контактные формируют тревожное извещение при нормированном ударном воздействии на контролируемую поверхность охраняемого объекта. Они предназначены для обнаружения раз ...