Расчет выходного сигнала в частотной области с помощью алгоритма БПФ и выходного сигнала во временной области с помощью алгоритма ОБПФ

Для нахождения Y(jkw1) предварительно, используя алгоритм «бабочка», найдем последовательность отсчетов входного сигнала в частотной области X(jkw1).

Формула БПФ для входного сигнала:

,

где N - количество отсчетов во временной и частотной областях; - весовая функция. Стандартные размеры оградки на могилу Компания Карелия.

Последовательность отсчетов во временной области X(nT) имеет вид:(nT) = {0,83; -0,9; -0,39; 0,68; -0,21; 0; -0,17 ;0,27}

Нахождение последовательности X(jkw1) производится аналогично расчету H(jkw1). Метод «бабочки» для нахождения X(jkw1) показан на рис.7.

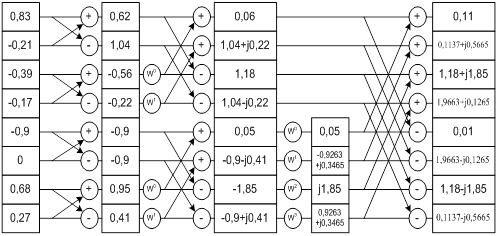
Рисунок 7 - Алгоритм «бабочка» для расчёта X(jkw1).

В результате расчетов получили следующую последовательность:

(jkw1) = {0,11; 0,1137+j0,5665; 1,18+j1,85; 1,9663+j0,1265; 0,01; 1,9663-j0,1265; 1,18-j1,85; 0,1137-j0,5665}

(jkw1) определяем из выражения для передаточной функции:

, .

Последовательности H(jkw1) и X(jkw1) были определены ранее:

(jkw1) = {0,11; 0,1137+j0,5665; 1,18+j1,85; 1,9663+j0,1265; 0,01; 1,9663-j0,1265; 1,18-j1,85; 0,1137-j0,5665}(jkw1) = {1,9267; 0,0022-j0,1906; 0,5613+j1,6832; 1,2688-j0,5292; 0,7287; 1,2688+j0,5292 ; 0,5613-j1,6832; 0,0022+j0,1906}

Перемножив почленно X(jkw1) и H(jkw1) найдем Y(jkw1):

Y(jkw1)= {0,2119; 0,1082-j0,0205; -2,4516+j3,0246; 2,5618-j0,8801; 0,0073; 2,5618+j0,8801; -2,4516-j3,0246; 0,1082+j0,0205}

Зная последовательность отсчетов выходного сигнала в частотной области Y(jkw1) с помощью алгоритма ОБПФ найдем выходной сигнал во временной области Y(nT). Таким образом, мы осуществим проверку правильности нахождения выходного сигнала по формуле круговой свертки.

Формула ОБПФ для выходного сигнала:

,

где N - количество отсчетов во временной и частотной областях; - весовая функция.

При расчете Y(nT) исходной последовательностью будет являться последовательность отсчетов входного сигнала в частотной области Y(jkw1).(jkw1) была определена ранее с помощью алгоритма БПФ.

Количество отсчетов N=8, поэтому ОБПФ, как и БПФ производится в три этапа. Определяем для каждого из этапов значения весовых функций.

Этап 1. Количество взаимодействующих элементов - 2:

== 1 .

Этап 2. Количество взаимодействующих элементов - 4:

== 1 ; W1=== +j

Этап 3. Количество взаимодействующих элементов - 8:

W0== 1 ; W1=== 0,7071 + j 0,7071 ; W2=== +j ,=== - 0,7071 + j 0,7071 .

Алгоритм ОБПФ аналогичен алгоритму БПФ. Результаты вычислений приведены на рис.8.

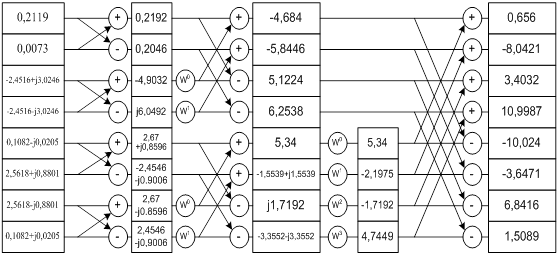
Рисунок 8 - Алгоритм «бабочка» для расчёта Y(jkw1) по ОБПФ

Полученные в результате вычислений ОБПФ значения Y(nT) должны быть разделены на N.

При N=8 получаем следующую последовательность:

(nT)={0,082;-1,0053;0,4254;1,3748;-1,253;-0,4559;0,8552;0,1886}

Как видно последовательность отчетов выходного сигнала во временной области с учетом неизбежной погрешности округления совпадает с последовательностью, рассчитанной методом круговой свертки.

Читайте также

Обучающая подсистема для лабораторного исследования характеристик замкнутых САУ в среде интернет
В последние десятилетия в зарубежных системах образования произошли существенные изменения, обусловленные бурным развитием научно-технического прогресса и его воздейст ...

Разработка комплекта электрических схем маршрутной релейной централизации блочного типа
Целью дипломного проектирование являлась разработка комплекта электрических схем маршрутной релейной централизации блочного типа (БМРЦ) для использования их студентами техникума в качест ...

Оценка производительности каналов и мониторинг корпоративной сети
В последнее время всё чаще документооборот и передача корпоративной информации совершается в электронном виде тем или иным способом. Для этого уже существует множество протоколов и метод ...