Частотные показатели качества переходных процессов

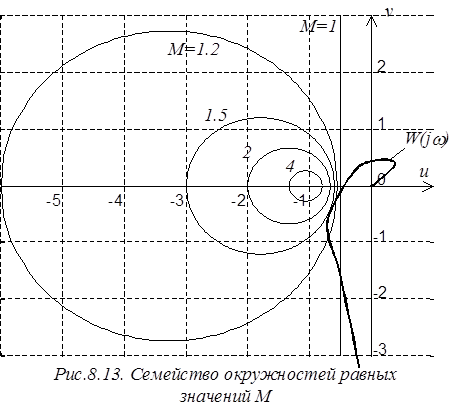
Можно отметить, что для значений 0<M<1 получится семейство окружностей, расположенный справа от прямой М=1 симметрично с первым семейством. При М=0 окружность вырождается в точку, совпадающую с началом координат.

Величина резонансного максимума может быть определена путем нахождения окружности, которой касается ЧХ разомкнутой САР (совпадает только в одной точке). Например, САР, ЧХ которой в разомкнутом состоянии имеет вид W(jw) (рис.8.13) будет иметь резонансный максимум Мр=1.5.

Проектирование САР с заданным уровнем Мр

На практике очень часто ставят задачу: спроектировать систему, для которой Мр будет не больше некоторого заданного значения Mзад. Очевидно, что в общем случае задача будет решена, если обеспечить такой вид ЧХ разомкнутой системы, чтобы ее кривая не заходила внутрь окружности М=Мзад (рис.8.14). Таким образом, окружность М=Мзад ограничивает запретную зону для амплитудно-фазовой характеристики (заштрихована).

Рассмотрим частный случай. Пусть Мзад=2.

Решение.

По заданной величине Мзад определяем координаты радиуса и центра окружности:

; .

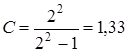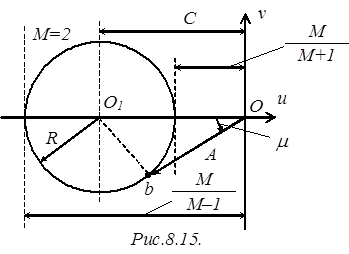
Строим окружность с центром в точке (-1,33; 0) радиуса 0,67 (рис.8.15).

Чтобы реальное значение резонансного максимума было меньше заданного, необходимо, чтобы ЧХ разомкнутой САР не заходила в запретную зону, т.е. внутрь окружности.

Пусть точка b принадлежит ЧХ разомкнутой САР. Обозначим угол, который образует вектор А, проведенный из начала координат в точку b, с отрицательным направлением оси u, через m. Очевидно, что угол m равен запасу устойчивости САР по фазе.

Из рис.8.15 следует, что запретная зона может иметь место при значении модуля АЧХ А разомкнутой системы

или

. (5)

Очевидно также, что для любого модуля А существует такой угол m, при котором ЧХ разомкнутой системы не заходит в запретную зону.

Из треугольника ObO1 можно найти выражение для запаса по фазе, при котором ЧХ может попасть в запретную зону:

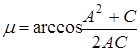. (6)

Используя (6), можно построить называемые m-кривые (рис.8.16) [1], пользуясь которыми, для любого значения модуля А можно найти то значение величины m, при котором обеспечивается требуемое значение резонансного максимума.

Для зависимости (6) можно определить, что максимум будет иметь место при , а само значение максимума:

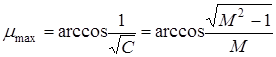. (7)

Если имеются логарифмические частотные характеристики разомкнутой системы, то по имеющимся m-кривым и при заданном значении М можно построить требуемое значение запаса по фазе для каждого значения модуля А, удовлетворяющего условию (5), которое для ЛАЧХ принимает вид:

. (8)

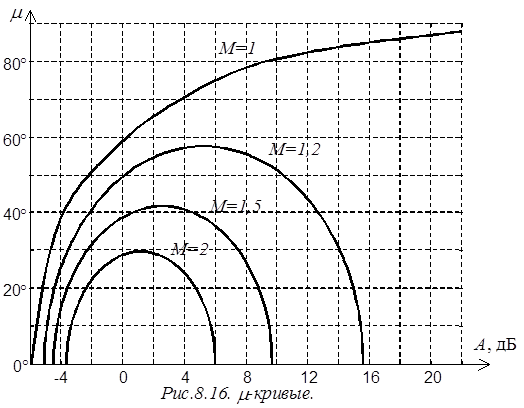
В результате можно получить запретную зону для ЛФЧХ. Чтобы показатель колебательности Мр не был больше заданного значения, ЛФЧХ не должна заходить в эту область.

Определим условия, при которых ЛФЧХ гарантированно не заходит в запретную область, на примере типовой ЛАЧХ типа "-2-1-2".

Пусть передаточная функция разомкнутой САР равна

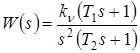, (9)

причем .

Логарифмические частотные характеристики такой разомкнутой САР представлены на рис.8.17.

Выражение для ЛФЧХ для (9) имеет вид:

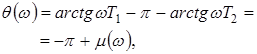
где - запас по фазе, который запишем следующим образом:

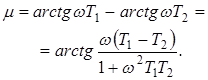(10)

Читайте также

Проект цифрового фильтра
В последнее время методы цифровой обработки сигналов (ЦОС) в радиотехнике, системах связи, управления и контроля приобрели большую важность и в значительной мере заменяют классические а ...

Разработка компьютерной сети по технологии Token Ring c STP с подключением к Интернет
Организация компьютерных сетей: Назначение КС - КС используется для объединения ПК, программно-аппаратных комплексов и связующих линий, обеспечивающих обмен информации. КС использует ...

Проектирование системы автоматического управления очистки стекла спортивного самолета
Задачи по управлению тем или иным явлением или процессом, возникающие в повседневной практической деятельности человека обширны и многообразны. Управление можно определить как совоку ...